- 动规讲解基础讲解三——混合背包（背包模板）

news/2024/11/14 10:59:23

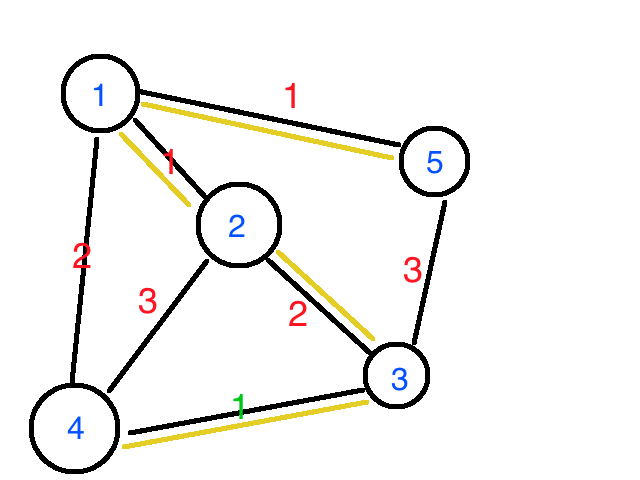
将01背包，完全背包，和多重完全背包问题结合起来，那么就是混合三种背的问题

根据三种背包的思想，那么可以得到
混合三种背包的问题可以这样子求解
　　for(int i=1; i<=N; ++i)
　　　　if(第i件物品是01背包)
　　　　　　zeroOnePack(c[i],w[i]);
　　　　else if(第i件物品是完全背包)
　　　　　　completePack(c[i],w[i]);
　　　　else if(第i件物品是多重完全背包)
　　　　　　multiplePack(c[i],w[i],n[i]);
这样能得到最优解的原因是，因为前一层已经是得到最优解了，
当前层求解最优解的时候，我们考虑要使用三种背包中的哪一种方法
而不用考虑前一层是怎么得到最优解的

#include <stdio.h>
#include <string.h>
int cash;
int n[11],dk[11];
int dp[1000000];
inline int max(const int &a, const int &b)
{
    return a < b ? b : a;
}
void CompletePack(int cost)
{
    for(int i=cost; i<=cash; ++i)
        dp[i] = max(dp[i],dp[i-cost]+cost);
}
void ZeroOnePack(int cost)
{
    for(int i=cash; i>=cost; --i)
        dp[i] = max(dp[i],dp[i-cost]+cost);
}
void MultiplePack(int cnt, int cost)
{
    if(cnt*cost >=cash)//如果第i种物品的费用总和超过背包容量，那么就是完全背包问题
        CompletePack(cost);
    else
    {
        int k = 1;//二进制拆分
        while(k<cnt)//判断剩下的数字能不能够拆分为k
        {
            ZeroOnePack(cost*k);
            cnt -=k;
            k<<=1;
        }
        ZeroOnePack(cnt*cost);
    }
}
int main()
{
    //输入的处理以及函数的调用
    return 0;
}